Coppersmith's attack
Coppersmith útok popisuje třídu útoků na veřejného klíče kryptografickéhoRSA na základě teorému Coppersmith tyto (viz níže). Veřejný klíč v systému RSA je n-tice celých čísel 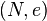 , kde N je součin dvou prvočísel p a q .Tajný klíč je dána tím, celé číslo d uspokojující
, kde N je součin dvou prvočísel p a q .Tajný klíč je dána tím, celé číslo d uspokojující 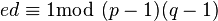 , ekvivalentně, může tajný klíč bude dána
, ekvivalentně, může tajný klíč bude dána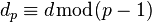 a
a  v případě, že čínská věta o zbytku se používá ke zlepšení rychlosti dekódování, viz CRT-rsa . Šifrování azprávy M produkuje ciphertext
v případě, že čínská věta o zbytku se používá ke zlepšení rychlosti dekódování, viz CRT-rsa . Šifrování azprávy M produkuje ciphertext 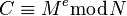 , které mohou být dešifrovat pomocí
, které mohou být dešifrovat pomocí  výpočtem
výpočtem 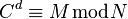 .
.
Coppersmith věta má mnoho aplikací v útoku RSA zvláště pokud veřejný exponent e je malý, nebo pokud částečná znalost tajného klíče je k dispozici.
[ editovat ]Nízká veřejný exponent útok
Za účelem snížení šifrování nebo podpis - ověření doby, je vhodné použít malý veřejnou exponent (  ). V praxi, společné možnosti pro
). V praxi, společné možnosti pro  jsou 3, 17 a 65537
jsou 3, 17 a 65537  . [ 1 ] Tyto hodnoty pro e jsou Fermatova prvočísla , někdy označované jako
. [ 1 ] Tyto hodnoty pro e jsou Fermatova prvočísla , někdy označované jako 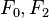 a
a  , resp
, resp  . Jsou vybrány, protože oni dělají modulární umocňování operace rychleji. Také, co si vyberete jako
. Jsou vybrány, protože oni dělají modulární umocňování operace rychleji. Také, co si vyberete jako  , že je jednodušší ověřit, zda
, že je jednodušší ověřit, zda  a
a  při generování a testování prvočísel v kroku 1generování klíčů . Hodnoty
při generování a testování prvočísel v kroku 1generování klíčů . Hodnoty  nebo
nebo  že selhání tento test může být zamítnuta tam a pak. (Ještě lepší: pokud e je prvočíslo a větší než 2, pak zkouška
že selhání tento test může být zamítnuta tam a pak. (Ještě lepší: pokud e je prvočíslo a větší než 2, pak zkouška 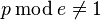 může nahradit dražší testu
může nahradit dražší testu  .
.
Pokud veřejný exponent je malý a holý  je velmi krátký, pak RSA funkce mohou být snadno invertovat což některé útoky možné. polstrování systémyzajistí, že zprávy mají plné délky, ale navíc volbě veřejného exponentu
je velmi krátký, pak RSA funkce mohou být snadno invertovat což některé útoky možné. polstrování systémyzajistí, že zprávy mají plné délky, ale navíc volbě veřejného exponentu  se doporučuje. Pokud se používá tato hodnota, ověřování podpisu vyžaduje 17 násobení, jak protichůdný k zhruba 1000, kdy náhodný
se doporučuje. Pokud se používá tato hodnota, ověřování podpisu vyžaduje 17 násobení, jak protichůdný k zhruba 1000, kdy náhodný  se používá stejné velikosti. rozdíl nízké soukromý exponent (viz Wienerova útoku ), útoky, které se použijí v případě malé
se používá stejné velikosti. rozdíl nízké soukromý exponent (viz Wienerova útoku ), útoky, které se použijí v případě malé  použití jsou daleko od celkového přestávky , které by navrácení tajný klíč d. . Nejsilnější útoky na nízkou míru veřejného exponentu RSA jsou založeny na následující věta, která je vzhledem k Don Coppersmith .
použití jsou daleko od celkového přestávky , které by navrácení tajný klíč d. . Nejsilnější útoky na nízkou míru veřejného exponentu RSA jsou založeny na následující věta, která je vzhledem k Don Coppersmith .
Nechť N je celé číslo a ![f \ in {\ mathbb Z} [x]](http://upload.wikimedia.org/math/0/4/1/041c300e1899b19ab48add9ab57ea036.png) je monic polynom stupně
je monic polynom stupně  nad celými čísly. Nastavit
nad celými čísly. Nastavit  pro
pro 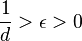 . Pak, stejně
. Pak, stejně  může útočník, Eve, efektivně najít celá čísla
může útočník, Eve, efektivně najít celá čísla  uspokojující
uspokojující 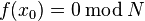 . Doba chodu dominuje čas potřebný ke spuštěníLLL algoritmus na mřížce o rozměru O
. Doba chodu dominuje čas potřebný ke spuštěníLLL algoritmus na mřížce o rozměru O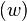 s
s  .
.
Tato věta uvádí existenci algoritmu , který může efektivně najít všechny kořenyna  modulo
modulo  , které jsou menší než
, které jsou menší než  . Jak
. Jak  se zmenší, bude algoritmu runtime snížit. Tato věta je síla je schopnost najít všechny malé kořeny polynomů modulo složené
se zmenší, bude algoritmu runtime snížit. Tato věta je síla je schopnost najít všechny malé kořeny polynomů modulo složené  .
.
[ upravit překlad ]Håstad tyto Broadcast útoku
Nejjednodušší forma útoku Håstad je je předložen usnadňují pochopení.Obecný případ využívá Coppersmith větu.
Předpokládejme, že jednoho odesílatele odešle stejnou zprávu  v zašifrované podobě na počtu lidí
v zašifrované podobě na počtu lidí  , z nichž každý se stejným malý veřejný exponent
, z nichž každý se stejným malý veřejný exponent  , říkají
, říkají 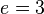 , a různé moduly
, a různé moduly 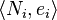 . Jednoduchý argument ukáže, že jakmile
. Jednoduchý argument ukáže, že jakmile  ciphertexts jsou známy, zpráva
ciphertexts jsou známy, zpráva  je již bezpečný: Předpokládejme Eve zachytí
je již bezpečný: Předpokládejme Eve zachytí  , a
, a 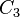 , kde
, kde 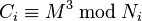 . Můžeme se domnívat,
. Můžeme se domnívat,  pro všechny
pro všechny  (jinak, je možné vypočítat faktor jednoho z
(jinak, je možné vypočítat faktor jednoho z  "s tím, že počítá
"s tím, že počítá 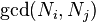 .) Do čínské věty o zbytcích , může si spočítat
.) Do čínské věty o zbytcích , může si spočítat 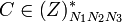 tak, že
tak, že 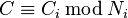 . Pak
. Pak 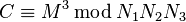 , nicméně, protože
, nicméně, protože  pro všechny
pro všechny  ", máme
", máme  . Tak
. Tak 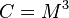 má přes celá čísla, a Eva mohou vypočítat třetí odmocninu z
má přes celá čísla, a Eva mohou vypočítat třetí odmocninu z  získat
získat  .
.
Pro větší hodnoty  více ciphertexts jsou zapotřebí, a to zejména,
více ciphertexts jsou zapotřebí, a to zejména,  ciphertexts jsou dostatečné.
ciphertexts jsou dostatečné.
[ editovat ]Zevšeobecňování
Håstad také ukázal, že použití lineární - padding , aby  před šifrování nechrání proti tomuto útoku. Předpokládejme, že útočník dozví, že
před šifrování nechrání proti tomuto útoku. Předpokládejme, že útočník dozví, že 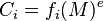 pro
pro  a některé lineární funkce
a některé lineární funkce 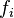 , tj., Bob použije podložku na zprávy
, tj., Bob použije podložku na zprávy  před šifrováním tak, aby příjemci obdrží mírně odlišné zprávy. Například, pokud
před šifrováním tak, aby příjemci obdrží mírně odlišné zprávy. Například, pokud  je
je  bitů dlouhé, může Bob šifrování
bitů dlouhé, může Bob šifrování 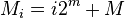 a poslat to do i -tého příjemce.
a poslat to do i -tého příjemce.
Pokud dostatečně velká skupina lidí se účastní, může útočník obnovit holý  ze všech ciphertext s podobnými metodami. Ve více obecnosti, Håstad prokázáno, že systém jednorozměrných rovnic modulo nesoudělná kompozitů, například použitím jakékoli pevné polynomiální
ze všech ciphertext s podobnými metodami. Ve více obecnosti, Håstad prokázáno, že systém jednorozměrných rovnic modulo nesoudělná kompozitů, například použitím jakékoli pevné polynomiální 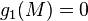 mod
mod  , by mohla být vyřešena, pokud dostatečně mnoho rovnic jsou k dispozici. Tentoútok naznačuje, že randomizované výplň by měl být použit ve šifrování RSA .
, by mohla být vyřešena, pokud dostatečně mnoho rovnic jsou k dispozici. Tentoútok naznačuje, že randomizované výplň by měl být použit ve šifrování RSA .
[ editovat ]Věta 2 (Håstad)
Předpokládejme, že 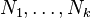 jsou nesoudělná celá čísla a nastavení
jsou nesoudělná celá čísla a nastavení 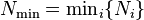 . Nechť
. Nechť ![g_i (x) = \ in \ mathbb {Z} / N_i \ left [x \ right]](http://upload.wikimedia.org/math/f/3/d/f3dcf999a410867ef9b3e8fa5f085d42.png) je k. polynomymaximálního stupně
je k. polynomymaximálního stupně  . Předpokládejme, že existuje jedinečná
. Předpokládejme, že existuje jedinečná 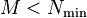 uspokojující
uspokojující  (mod
(mod  ) pro všechny
) pro všechny  . Dále předpokládám
. Dále předpokládám  . K dispozici je efektivníalgoritmus , který vzhledem k tomu,
. K dispozici je efektivníalgoritmus , který vzhledem k tomu,  pro všechny
pro všechny  , počítá
, počítá  .
.
Důkaz :
Vzhledem k tomu,  jsou nesoudělná čínská věta o zbytcích by mohly být použity pro výpočet koeficientů
jsou nesoudělná čínská věta o zbytcích by mohly být použity pro výpočet koeficientů  uspokojující
uspokojující 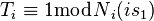 a
a  pro všechny
pro všechny  . Nastavení
. Nastavení  víme, že
víme, že 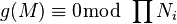 .Vzhledem k tomu,
.Vzhledem k tomu,  jsou nenulová jsme, že
jsou nenulová jsme, že 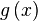 je také nenulová. Stupeň
je také nenulová. Stupeň 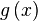 je nejvíce
je nejvíce  . Podle Věty Coppersmith je, můžeme spočítat všechnyceločíselné kořeny
. Podle Věty Coppersmith je, můžeme spočítat všechnyceločíselné kořeny  splňují
splňují  a
a 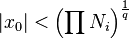 . Nicméně, my víme, že
. Nicméně, my víme, že  , takže
, takže  je mezi kořeny nalezených věty Coppersmith je.
je mezi kořeny nalezených věty Coppersmith je.
Tato věta může být použita k problému vysílání RSA následujícím způsobem: Předpokládejme i -tý holý je naplněn polynomu  , tak, že
, tak, že 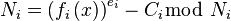 . Pak polynomy
. Pak polynomy 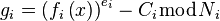 splňují tento vztah. Útok uspěje jednou
splňují tento vztah. Útok uspěje jednou  . Původní výsledek používal na Håstad metodu namísto plného Coppersmith metodu. Jeho výsledek byl vyžadován
. Původní výsledek používal na Håstad metodu namísto plného Coppersmith metodu. Jeho výsledek byl vyžadován  zprávy, kde
zprávy, kde 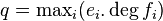 . [ 3 ]
. [ 3 ]
[ upravit překlad ]Franklin-Reiter Související zprávy útoku
Franklin-Reiter poznal nový útok proti RSA s veřejným exponentem 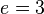 .Jestliže dvě zprávy se liší pouze známým pevnou rozdílu mezi oběma zpráv a jsou RSA šifrované za stejných RSA modulu
.Jestliže dvě zprávy se liší pouze známým pevnou rozdílu mezi oběma zpráv a jsou RSA šifrované za stejných RSA modulu  , pak je možné získat oba.
, pak je možné získat oba.
[ editovat ]Jak to funguje?
Nechť 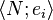 je Alicin veřejný klíč. Předpokládejme, že
je Alicin veřejný klíč. Předpokládejme, že 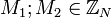 jsou dvě odlišné zprávy splňující
jsou dvě odlišné zprávy splňující  nějakou veřejně známou polynomu
nějakou veřejně známou polynomu ![f \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/2/6/8/268eb275484134518be3f82e81189a8f.png) . Chcete-li odeslat
. Chcete-li odeslat 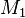 a
a  Alici, může Bob naivně šifrování na zprávy a předá výsledné ciphertexts
Alici, může Bob naivně šifrování na zprávy a předá výsledné ciphertexts  . Eve si můžete snadno obnovit
. Eve si můžete snadno obnovit 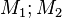 , stejně
, stejně  , pomocí následující větu:
, pomocí následující větu:
[ editovat ]Věta 3 (Franklin-Reiter)
Nastavit 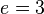 a nechat
a nechat  se RSA veřejný klíč. Nechte
se RSA veřejný klíč. Nechte  uspokojit
uspokojit  nějakou lineární polynom
nějakou lineární polynom ![f = ax + b \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/4/8/8/488f73c2b63a757a35f697dd87508197.png) s
s 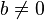 . Pak, stejně
. Pak, stejně 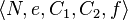 může útočník, Eve, obnovit
může útočník, Eve, obnovit 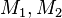 v časovémkvadratický v
v časovémkvadratický v  .
.
Pro libovolné  (spíše než omezení na
(spíše než omezení na 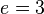 ) potřebný čas je kvadratický v
) potřebný čas je kvadratický v  a
a  ).
).
Důkaz :
Vzhledem k tomu,  víme, že
víme, že  je kořen z polynomu
je kořen z polynomu ![g_1 (x) = f (x) ^ e - c_1 \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/b/c/e/bce099504b4b012646086236c91d9709.png) . Podobně,
. Podobně,  je kořen
je kořen ![g_2 (x) = x ^ e-c_2 \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/a/3/b/a3ba064443e02f115c25f4540c9dd79a.png) . Lineární součinitel
. Lineární součinitel  rozděluje obě polynomů . Proto, Eva vypočítává největší společný dělitel (gcd) o
rozděluje obě polynomů . Proto, Eva vypočítává největší společný dělitel (gcd) o  a
a  , v případě, že gcd dopadá být lineární,
, v případě, že gcd dopadá být lineární,  se nachází. Gcd může být počítán v kvadratické času
se nachází. Gcd může být počítán v kvadratické času  a
a  pomocí Euclidean algoritmus .
pomocí Euclidean algoritmus .
[ upravit překlad ]Coppersmith tyto Short Pad útoku
Stejně jako Håstad je a Franklin Reiter útoku, tento útok využívá slabost RSA s veřejným exponentem 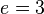 . Coppersmith ukázal, že pokud randomizované padding navrhl Håstad se používá nesprávně pak RSA šifrování není bezpečné.
. Coppersmith ukázal, že pokud randomizované padding navrhl Håstad se používá nesprávně pak RSA šifrování není bezpečné.
[ editovat ]Jak to funguje?
Předpokládejme, že Bob pošle zprávu  Alici pomocí malého náhodného polstrování před zašifrováním to. Útočník, Eve, zachytí šifrový text a zabraňuje jeho dosažení svého cíle. Bob se rozhodne odeslat
Alici pomocí malého náhodného polstrování před zašifrováním to. Útočník, Eve, zachytí šifrový text a zabraňuje jeho dosažení svého cíle. Bob se rozhodne odeslat  Alici, protože Alice nereagoval na jeho poselství. On náhodně podložky
Alici, protože Alice nereagoval na jeho poselství. On náhodně podložky  znovu a přenáší výsledný šifrovaný. Eva má nyní dva ciphertexts odpovídající dvěma šifrování stejné zprávy pomocí dvou různých náhodných vycpávky.
znovu a přenáší výsledný šifrovaný. Eva má nyní dva ciphertexts odpovídající dvěma šifrování stejné zprávy pomocí dvou různých náhodných vycpávky.
I když Eva neví, náhodné podložku používán, pořád může obnovit zprávu  pomocí následující větu, pokud náhodná výplň je příliš krátký.
pomocí následující větu, pokud náhodná výplň je příliš krátký.
[ editovat ]Věta 4 (Coppersmith)
Nechť  je veřejný RSA klíč kde
je veřejný RSA klíč kde  je
je  -bitů. Nastavit
-bitů. Nastavit 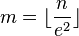 .Nechť
.Nechť  je zpráva délky u většiny
je zpráva délky u většiny  bitů. Definovat
bitů. Definovat  a
a  , kde
, kde 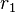 a
a 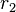 je odlišnécelá čísla s
je odlišnécelá čísla s 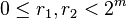 . Pokud Marvin je dána
. Pokud Marvin je dána  a šifrování
a šifrování s
s 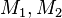 (ale není uveden
(ale není uveden 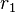 , nebo
, nebo 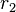 , může efektivně obnovit
, může efektivně obnovit  .
.
Důkaz [ 2 ]
Definovat  a
a  . Víme, že když
. Víme, že když  tyto polynomy mají
tyto polynomy mají  jako společný kořen.Jinými slovy,
jako společný kořen.Jinými slovy, 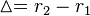 je kořen výslednice
je kořen výslednice ![h (y) = {\ rm res} _x (g_1, g_2) \ in \ mathbb {Z} _N [y]](http://upload.wikimedia.org/math/1/1/3/11384f5a5a3d442af180c87ca0b7c8cb.png) . Kromě toho,
. Kromě toho,  .Proto,
.Proto, 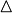 je malý kořen
je malý kořen  modulo
modulo  , a Marvin může efektivně najít pomocí Věty 1 (Coppersmith) . Jakmile
, a Marvin může efektivně najít pomocí Věty 1 (Coppersmith) . Jakmile 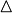 je známo, Franklin-Reiter útok může být použita k obnovení
je známo, Franklin-Reiter útok může být použita k obnovení  a následně
a následně  .
.
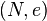 , kde N je součin dvou prvočísel p a q .Tajný klíč je dána tím, celé číslo d uspokojující
, kde N je součin dvou prvočísel p a q .Tajný klíč je dána tím, celé číslo d uspokojující 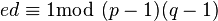 , ekvivalentně, může tajný klíč bude dána
, ekvivalentně, může tajný klíč bude dána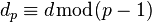 a
a  v případě, že čínská věta o zbytku se používá ke zlepšení rychlosti dekódování, viz CRT-rsa . Šifrování azprávy M produkuje ciphertext
v případě, že čínská věta o zbytku se používá ke zlepšení rychlosti dekódování, viz CRT-rsa . Šifrování azprávy M produkuje ciphertext 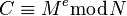 , které mohou být dešifrovat pomocí
, které mohou být dešifrovat pomocí  výpočtem
výpočtem 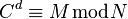 .
. ).
). .
.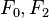 a
a , resp
, resp .
. a
a při generování a testování prvočísel v kroku 1
při generování a testování prvočísel v kroku 1 nebo
nebo že selhání tento test může být zamítnuta tam a pak.
že selhání tento test může být zamítnuta tam a pak.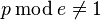 může nahradit dražší testu
může nahradit dražší testu .
.
 se doporučuje. Pokud se používá tato hodnota, ověřování podpisu vyžaduje 17 násobení, jak protichůdný k zhruba 1000, kdy náhodný
se doporučuje. Pokud se používá tato hodnota, ověřování podpisu vyžaduje 17 násobení, jak protichůdný k zhruba 1000, kdy náhodný![f \ in {\ mathbb Z} [x]](http://upload.wikimedia.org/math/0/4/1/041c300e1899b19ab48add9ab57ea036.png) je
je pro
pro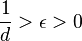 .
. může útočník, Eve, efektivně najít celá čísla
může útočník, Eve, efektivně najít celá čísla uspokojující
uspokojující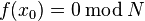 .
.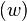
 .
. modulo
modulo , které jsou menší než
, které jsou menší než .
. se zmenší, bude algoritmu runtime snížit.
se zmenší, bude algoritmu runtime snížit. v zašifrované podobě na počtu lidí
v zašifrované podobě na počtu lidí , z nichž každý se stejným malý veřejný exponent
, z nichž každý se stejným malý veřejný exponent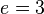 , a různé moduly
, a různé moduly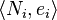 .
. ciphertexts jsou známy, zpráva
ciphertexts jsou známy, zpráva , a
, a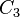 , kde
, kde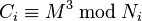 .
. pro všechny
pro všechny (jinak, je možné vypočítat
(jinak, je možné vypočítat "s tím, že počítá
"s tím, že počítá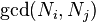 .) Do
.) Do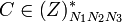 tak, že
tak, že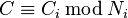 .
.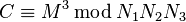 , nicméně, protože
, nicméně, protože pro všechny
pro všechny ", máme
", máme .
.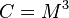 má přes celá čísla, a Eva mohou vypočítat
má přes celá čísla, a Eva mohou vypočítat získat
získat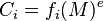 pro
pro a některé lineární funkce
a některé lineární funkce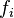 , tj., Bob použije
, tj., Bob použije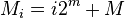
 ze všech
ze všech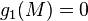
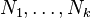 jsou
jsou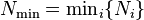 .
.![g_i (x) = \ in \ mathbb {Z} / N_i \ left [x \ right]](http://upload.wikimedia.org/math/f/3/d/f3dcf999a410867ef9b3e8fa5f085d42.png) je
je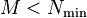 uspokojující
uspokojující (mod
(mod .
. .
. pro všechny
pro všechny
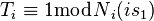 a
a pro všechny
pro všechny .
. víme, že
víme, že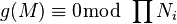 .Vzhledem k tomu,
.Vzhledem k tomu,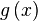 je také nenulová.
je také nenulová. splňují
splňují a
a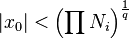 .
. , takže
, takže , tak, že
, tak, že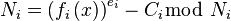 .
.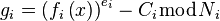 splňují tento vztah.
splňují tento vztah. .
. zprávy, kde
zprávy, kde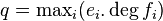 .
.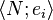 je Alicin veřejný klíč.
je Alicin veřejný klíč.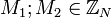 jsou dvě odlišné
jsou dvě odlišné nějakou veřejně známou
nějakou veřejně známou![f \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/2/6/8/268eb275484134518be3f82e81189a8f.png)
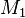 a
a Alici, může Bob naivně
Alici, může Bob naivně
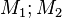 , stejně
, stejně se RSA veřejný klíč.
se RSA veřejný klíč. uspokojit
uspokojit![f = ax + b \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/4/8/8/488f73c2b63a757a35f697dd87508197.png)
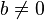 .
.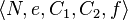 může útočník, Eve, obnovit
může útočník, Eve, obnovit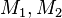 v časovém
v časovém .
. víme, že
víme, že![g_1 (x) = f (x) ^ e - c_1 \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/b/c/e/bce099504b4b012646086236c91d9709.png)
![g_2 (x) = x ^ e-c_2 \ in \ mathbb {Z} _N [x]](http://upload.wikimedia.org/math/a/3/b/a3ba064443e02f115c25f4540c9dd79a.png) .
. rozděluje obě
rozděluje obě a
a , v případě, že gcd dopadá být lineární,
, v případě, že gcd dopadá být lineární, -bitů.
-bitů.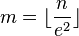 .Nechť
.Nechť je zpráva délky u většiny
je zpráva délky u většiny bitů.
bitů. a
a , kde
, kde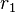 a
a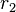 je
je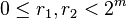 .
. a
a .
. tyto
tyto jako společný kořen.Jinými slovy,
jako společný kořen.Jinými slovy,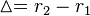 je kořen
je kořen![h (y) = {\ rm res} _x (g_1, g_2) \ in \ mathbb {Z} _N [y]](http://upload.wikimedia.org/math/1/1/3/11384f5a5a3d442af180c87ca0b7c8cb.png)
 .Proto,
.Proto, je malý kořen
je malý kořen modulo
modulo