Correlation Attack
V kryptografii , korelační útoky jsou třída známých holého útoků na lámáníproudových šifer , jejichž keystream je generován tím, že kombinuje výstup několika lineárních registrů zpětnovazební posuvný (tzv. LFSRs pro zbytek tohoto článku) pomocí logický funkce . Korelační útoky využít statistickou slabost, která plyne z chudé výběru Boolean funkce - je možné zvolit funkci, která se vyhýbá srovnávací útoky, takže tento typ šifry není ze své podstaty nebezpečné. Je to prostě důležité zvážit citlivost na srovnávací útoky při navrhování proudových šifer tohoto typu. [ pochvalná zmínka potřebovaný ]
Korelační útoky jsou možné, pokud je významná korelace mezi výstupním stavu jednoho individuálního LFSR v keystream generátoru a výstup Boolean funkce, která kombinuje výstupní stav všech LFSRs. V kombinaci s částečnou znalostí keystream (který je snadno odvodit z dílčích poznatků holého textu, jak dva jsou prostě XORed dohromady), což umožňuje útočníkovi brute-force klíč pro tento individuální LFSR a zbytek systému samostatně. Například, pokud v keystream generátoru, ve kterém jsou čtyři 8-bitové LFSRs kombinaci produkovat keystream, a jeden z registrů koreluje s booleovské funkce výstupu, můžeme hrubá síla je první a pak zbývající tři, pro celkem útok složitost 2 8 + 224 . Ve srovnání s náklady na zahájení pokusit útokem hrubou silou na celý systém, se složitostí 2 32 , což představuje útok úsilí úspory faktor 255, což je podstatné. Pokud druhý registr souvisí s funkcí, můžeme opakovat tento proces, a drop útoku na složitosti 2 8 + 2 8 + 2 16 za úsilí úspory faktor 65027.V tomto smyslu je možné korelační útoky za rozděl a panuj algoritmy .
Korelační útoky jsou možná nejlépe vysvětlit pomocí příkladu. Budeme uvažovat případ tzv. Geffe generátoru klíčů. Generátor Geffe se skládá ze tří LFSRs: LFSR-1, LFSR-2 a LFSR-3. Označíme-li výstupy těchto rejstříků  ,
,  a
a  , respektive, pak booleovská funkce, která kombinuje tři registry poskytnout výstup generátoru je dána tím,
, respektive, pak booleovská funkce, která kombinuje tři registry poskytnout výstup generátoru je dána tím,  (tj. (
(tj. (  A
A  ) XOR (NOT
) XOR (NOT  A
A  )). K dispozici jsou 2 3 = 8 možných hodnot pro výstupy tří registrů, a hodnota tohoto kombinuje funkce pro každý z nich je výstava v tabulce níže:
)). K dispozici jsou 2 3 = 8 možných hodnot pro výstupy tří registrů, a hodnota tohoto kombinuje funkce pro každý z nich je výstava v tabulce níže:
Booleovská funkce výstupní tabulka |  |  | 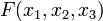 |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Uvažujme výstup třetího registru,  . Výše uvedená tabulka je jasné, že z 8 možných výstupů
. Výše uvedená tabulka je jasné, že z 8 možných výstupů  . 6 z nich jsou stejné na odpovídající hodnotu výkonu generátoru,
. 6 z nich jsou stejné na odpovídající hodnotu výkonu generátoru, 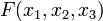 , tj.
, tj.  v 75% všech možných případů. Tak můžeme říci, že LFSR-3 je spojená s generátorem. To je slabost můžeme využít takto:
v 75% všech možných případů. Tak můžeme říci, že LFSR-3 je spojená s generátorem. To je slabost můžeme využít takto:
Předpokládejme, že zachytí ciphertext 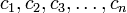 o otevřeném textu
o otevřeném textu , který byl šifrován pomocí proudu šifrou pomocí Geffe generátor jako jeho keystream generátoru, tj.
, který byl šifrován pomocí proudu šifrou pomocí Geffe generátor jako jeho keystream generátoru, tj.  pro
pro  , kde
, kde 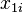 je výstup LFSR-1 v čase
je výstup LFSR-1 v čase  , atd. Dále předpokládejme, že víme, že některé části holý, např. víme
, atd. Dále předpokládejme, že víme, že některé části holý, např. víme  , že prvních 32 bitů otevřeného textu (odpovídá 4 znaky ASCII textu). To není tak nepravděpodobné, jak se to může zdát: víme-li, holý text je platný XML soubor, například víme, že první 4 znaky ASCII, musí být "<xml". Podobně jako toto, mnoho formáty souborů nebo síťové protokoly mají standardní záhlaví nebo zápatí, které mohou být uhodnuto snadno. Vzhledem k tomu, zachytil
, že prvních 32 bitů otevřeného textu (odpovídá 4 znaky ASCII textu). To není tak nepravděpodobné, jak se to může zdát: víme-li, holý text je platný XML soubor, například víme, že první 4 znaky ASCII, musí být "<xml". Podobně jako toto, mnoho formáty souborů nebo síťové protokoly mají standardní záhlaví nebo zápatí, které mohou být uhodnuto snadno. Vzhledem k tomu, zachytil  a naše známé / hádal
a naše známé / hádal  , můžeme snadno najít
, můžeme snadno najít 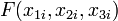 pro
pro  XORing dva spolu. Nyní víme, 32 po sobě jdoucích bitů výstupu generátoru.
XORing dva spolu. Nyní víme, 32 po sobě jdoucích bitů výstupu generátoru.
Nyní můžeme začít silovou hledání v prostoru možných klíčů (počáteční hodnoty) pro LFSR-3 (za předpokladu, že víme, že se závitem bity LFSR-3, předpoklad, který je v souladu se zásadou Kerckhoffs " ). Pro každý daný klíč v keyspace, můžeme rychle vytvářet prvních 32 bitů výstupu LFSR-3 je a porovnávat s našimi získaných 32 bitů z celého generátoru výstupu. Vzhledem k tomu, jsme založili již dříve, že je 75% korelace mezi výkonem LFSR-3 a generátorem, víme, že pokud jsme správně uhodl šipky na LFSR-3, cca 24 z prvních 32 bitů LFSR-3 výstup budou shodovat s odpovídajícími bity výstupu generátoru. Pokud jsme uhodli správně, měli bychom očekávat, že zhruba polovina, nebo 16, z prvních 32 bitů těchto dvou sekvencí, které vyhoví.Můžeme tedy obnovit tlačítko pro LFSR-3 nezávisle na klíče LFSR-1 a LFSR-2.V této fázi jsme snížili problém hovado nutit systém 3 LFSRs problému hovado nutit jednoho LFSR a pak se systém 2 LFSRs. Množství úsilí zde uložen, závisí na délce LFSRs. Pro realistické hodnoty, je velmi podstatné úspory a mohou brute force útoky velmi praktické.
Nepotřebujeme zde zastavit. Dodržujte v tabulce výše, která  rovněž souhlasí s výstupu generátoru 6 krát ze 8, opět korelace 75% korelace mezi
rovněž souhlasí s výstupu generátoru 6 krát ze 8, opět korelace 75% korelace mezi  a výkon generátoru. Můžeme začít pokusit útokem hrubou silou proti LFSR-2 nezávisle na klíče LFSR-1 a LFSR-3, takže jen LFSR-1 neporušený. Tak, jsme schopni zlomit Geffe generátor s co největší úsilí je třeba k hrubé síle 3 zcela nezávislé LFSRs, což znamená, že generátor Geffe je velmi slabý generátor a nikdy by neměly být použity k výrobě keystreams proudová šifra.
a výkon generátoru. Můžeme začít pokusit útokem hrubou silou proti LFSR-2 nezávisle na klíče LFSR-1 a LFSR-3, takže jen LFSR-1 neporušený. Tak, jsme schopni zlomit Geffe generátor s co největší úsilí je třeba k hrubé síle 3 zcela nezávislé LFSRs, což znamená, že generátor Geffe je velmi slabý generátor a nikdy by neměly být použity k výrobě keystreams proudová šifra.
Poznámka: z výše uvedené tabulky, která  souhlasí s výkonem generátoru 4 krát ze 8 - 50% srovnávací. Nemůžeme použít k hrubé síle LFSR-1 nezávisle na ostatních: správný klíč přinese výkon, který souhlasí s výstupu generátoru 50% času, ale v průměru tak bude nesprávné tlačítko. To představuje ideální situaci z hlediska bezpečnosti - kombinuje funkce
souhlasí s výkonem generátoru 4 krát ze 8 - 50% srovnávací. Nemůžeme použít k hrubé síle LFSR-1 nezávisle na ostatních: správný klíč přinese výkon, který souhlasí s výstupu generátoru 50% času, ale v průměru tak bude nesprávné tlačítko. To představuje ideální situaci z hlediska bezpečnosti - kombinuje funkce 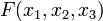 by měla být zvolena tak, aby vztah mezi každou proměnnou a kombinování funkce výkon je tak blízko, jak je to možné, aby 50%. V praxi může být obtížné najít funkci, která dosahuje tato aniž by byla obětována další konstrukční kritéria, např. doba v délce, tak kompromis může být nezbytné.
by měla být zvolena tak, aby vztah mezi každou proměnnou a kombinování funkce výkon je tak blízko, jak je to možné, aby 50%. V praxi může být obtížné najít funkci, která dosahuje tato aniž by byla obětována další konstrukční kritéria, např. doba v délce, tak kompromis může být nezbytné.
[ upravit překlad ]Objasnění statistické povahy útoku
Zatímco výše uvedený příklad dobře ilustruje poměrně jednoduché pojmy za srovnávací útoky, to možná zjednodušuje vysvětlení přesně, jak brutální nutit jednotlivých LFSRs výnosů. Vyrábíme prohlášení, že nesprávně tipoval klíče budou generovat LFSR výstup, který souhlasí s výstupu generátoru zhruba 50% času, protože stejně dva náhodné bitové posloupnosti dané délky, pravděpodobnost shody mezi sekvencí v každém konkrétním kousku je 0,5.Nicméně, může konkrétní individuální nesprávné klávesy a vytvářet LFSR výstup, který souhlasí s výstupu generátoru více či méně často než přesně 50% času. To je zvláště patrné iv případě LFSRs, jejichž korelace s generátorem není nijak zvlášť silný, pro malé dost korelací to rozhodně není mimo oblasti možnosti, že nesprávně odhadl klíč bude také vést k LFSR výstup, který souhlasí s požadovaným počtem bity výstupu generátoru. Tak jsme nemusí být schopni najít klíč k tomuto LFSR jednoznačně a s jistotou.Můžeme místo toho najít řadu možných klíčů, i když je to stále podstatné porušení šifry bezpečností. Kdybychom, řekněme, megabajt známého otevřeného textu, by se situace podstatně odlišná. Nesprávný klíč může generovat LFSR výstup, který souhlasí s více než 512 kilobajtů výkonu generátoru, ale není pravděpodobné, že generovat výstup, který souhlasí s jak hodně jako 768 KB na výstupu generátoru, jako správně odhadl klíč by.Zpravidla, slabší korelace mezi individuálním rejstříku a výkonu generátoru, je více známý holý nutné najít ten klíč registru se s vysokou mírou jistoty. Čtenáři se zázemím v teorii pravděpodobnosti by měl být schopen vidět, snadno, jak formalizovat tento argument a získat odhady délky známého otevřeného textu potřebné pro danou korelaci pomocí binomického rozdělení .
Korelace, které byly využívány v příkladu útoku na generátoru Geffe jsou příklady toho, co se nazývá prvního řádu korelace : jsou korelace mezi hodnotou výkonu generátoru a individuální LFSR. Je možné definovat vyšších řádů korelace kromě nich. Například, to může být možné, že zatímco stejně Booleovská funkce nemá žádné silné korelaci s některou z jednotlivých registrů spojuje, může významná korelace existuje mezi některými booleovské funkce dvou registrů, např. 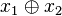 . To by byl příklad druhého řádu korelace .Můžeme definovat třetího řádu korelací a tak v explicitní formě.
. To by byl příklad druhého řádu korelace .Můžeme definovat třetího řádu korelací a tak v explicitní formě.
Vyšší útoky řád korelace může být silnější než jednotlivé útoky řádu korelace, ale tento účinek je předmětem "zákon omezení vrátí". Níže uvedená tabulka ukazuje míru výpočetní nákladů pro různé útoky na keystream generátoru se skládá z osmi 8-bitových LFSRs kombinaci jediným Boolean funkce. Principy výpočet nákladů je poměrně jednoduché: vlevo termín součtu představuje velikost keyspace pro srovnávaných generátorů, a nejvíce vpravo výraz představuje velikost keyspace pro zbývající generátorů.
Generátor útok úsilí| Útok | Snaha (velikost keyspace) |
|---|
Brute force | 
|
Single 1. řádu korelace útok | 
|
Single 2. řádu korelace útok | 
|
Single 3. řádu korelace útok | 
|
Single 4. řádu korelace útok | 
|
Single 5. objednávky korelace útok | 
|
Single 6. Aby vztah útok | 
|
Single 7. Aby korelace útok | 
|
While vyšších řádů korelace vést k silnější útoky, oni jsou také více obtížné najít, jako prostor dostupných logických funkcí korelovat proti zvýšení výkonu generátoru jako počet argumentů funkce dělá.
Booleovská funkce  na n proměnných je řekl, aby byl " m -tého řádu korelace imunní ", nebo mít" m -tého řádu srovnávací imunitu "pro nějaké celé číslo m , pokud není významná korelace mezi funkcí výstupu a některého Boolean funkce m ze svých vstupy. Například, booleovská funkce, která nemá žádné prvního pořadí nebo druhého řádu korelace, která však již třetího řádu korelace vykazuje 2. řádu srovnávací imunitu. Je zřejmé, že vyšší korelace imunita je funkce vhodnější pro použití v generátoru keystream (i když to není jediné, co je třeba vzít v úvahu).
na n proměnných je řekl, aby byl " m -tého řádu korelace imunní ", nebo mít" m -tého řádu srovnávací imunitu "pro nějaké celé číslo m , pokud není významná korelace mezi funkcí výstupu a některého Boolean funkce m ze svých vstupy. Například, booleovská funkce, která nemá žádné prvního pořadí nebo druhého řádu korelace, která však již třetího řádu korelace vykazuje 2. řádu srovnávací imunitu. Je zřejmé, že vyšší korelace imunita je funkce vhodnější pro použití v generátoru keystream (i když to není jediné, co je třeba vzít v úvahu).
Siegenthaler ukázala, že korelace imunita m z booleovské funkce algebraické studia d o n proměnných splňuje m + d ≤ n , pro daný soubor vstupních proměnných, to znamená, že vysoký stupeň algebraické omezí maximální možnou srovnávací imunitu. Kromě toho, v případě, že funkce je vyvážena pakm + d ≤ n -. 1 [ 1 ]
Z toho vyplývá, že není možné, aby funkce n proměnných n -tého řádu korelace imunní. To také vyplývá ze skutečnosti, že každý takový funkce může být napsáno pomocí Reed-Muller základ jako kombinace XORs o vstupních funkcí.
Vzhledem k tomu, případně extrémní závažnost korelace útoku jejího vlivu na proudový šifrovací klíč je bezpečnost, by mělo být považováno za nezbytné pro testování kandidáta logická kombinace funkcí pro srovnávací imunity před rozhodnutím použít v proudu šifry. Je však třeba poznamenat, že vysoká korelace imunita je nezbytné, ale ne postačující podmínkou pro logickou funkci jako vhodné pro použití ve keystream generátoru. Existují i jiné problémy, aby zvážila, např. zda je nebo není funkce je vyvážená - ať už výstupy tolik nebo hrubě tolik 1 je, jak to dělá 0 let, kdy se považují všechny možné vstupy.
Výzkum byl proveden v metod pro snadné generování logické funkce dané velikosti, které jsou zaručené mít alespoň nějakou zvláštní objednávku srovnávací imunity. Tento výzkum odhalil vazby mezi korelační imunitních booleovských funkcí a chyba kódy korigování . [ 2 ]
 ,
,  a
a  , respektive, pak booleovská funkce, která kombinuje tři registry poskytnout výstup generátoru je dána tím,
, respektive, pak booleovská funkce, která kombinuje tři registry poskytnout výstup generátoru je dána tím,  (tj. (
(tj. (  A
A  ) XOR (NOT
) XOR (NOT  A
A  )). K dispozici jsou 2 3 = 8 možných hodnot pro výstupy tří registrů, a hodnota tohoto kombinuje funkce pro každý z nich je výstava v tabulce níže:
)). K dispozici jsou 2 3 = 8 možných hodnot pro výstupy tří registrů, a hodnota tohoto kombinuje funkce pro každý z nich je výstava v tabulce níže: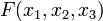
 v 75% všech možných případů.
v 75% všech možných případů.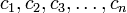 o otevřeném textu
o otevřeném textu , který byl šifrován pomocí proudu šifrou pomocí Geffe generátor jako jeho keystream generátoru, tj.
, který byl šifrován pomocí proudu šifrou pomocí Geffe generátor jako jeho keystream generátoru, tj. pro
pro , kde
, kde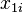 je výstup LFSR-1 v čase
je výstup LFSR-1 v čase , atd. Dále předpokládejme, že víme, že některé části holý, např. víme
, atd. Dále předpokládejme, že víme, že některé části holý, např. víme , že prvních 32 bitů otevřeného textu (odpovídá 4 znaky ASCII textu).
, že prvních 32 bitů otevřeného textu (odpovídá 4 znaky ASCII textu). a naše známé / hádal
a naše známé / hádal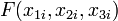 pro
pro XORing dva spolu.
XORing dva spolu.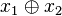 .
.







 na
na