
Index of coincidence
V kryptografii , náhoda, počítání je technika (vynalezl William F. Friedman[ 1 ] ) uvedení dva texty side-by-side a počítání, kolikrát, že identické dopisy se objeví na stejném místě v obou textech. Tento počet, a to buď jako poměr celkové nebo normalizačně vydělením očekávanou počtu pro náhodné zdrojového modelu, je známý jako index náhody .
Index náhodou je užitečné jak v analýze přírodních jazyce holého textu a při analýze ciphertext ( kryptoanalýza ). I když jen ciphertext je k dispozici pro testování a dopis holého textu identity jsou skryté, může náhody v ciphertext být způsobeny náhod v podkladové textu. Tato technika se používá kcryptanalyze na Vigenère kód , například. Pro opakování-klíče polyalphabetic kódu uspořádané do matice, bude náhoda rychlost v každém sloupci obvykle nejvyšší, pokud je šířka matice je násobkem délky klíče, a tato skutečnost může být použit k určení, délka klíče, který je Prvním krokem praskání systému.
Náhoda počítání může pomoci určit, kdy jsou dva texty napsány ve stejném jazyce pomocí stejné abecedu . (Tato technika byla použita, aby přezkoumala údajné Bible kód ). Kauzální náhoda počet takových textů bude výrazně vyšší než náhodné koincidenční počet pro texty v různých jazycích, nebo texty s využitím různých abeced, nebo blábol texty.
Chcete-li zjistit, proč, představte si "abecedu" z pouze ze dvou písmen A a B. Předpokládejme, že v našem "jazyk", dopis je používán 75% času, a písmeno B se používá 25% času. Pokud dva texty v tomto jazyce jsou položeny vedle sebe, pak tyto dvojice lze očekávat:
| Pár | Pravděpodobnost |
|---|---|
AA | 56,25% |
BB | 6,25% |
AB | 18,75% |
BA | 18,75% |
Celkově je pravděpodobnost "náhoda" je 62,5% (56,25% pro AA + 6,25% pro BB).
Nyní uvažujme případ, kdy obě zprávy jsou šifrovány pomocí jednoduchého monoalphabetic substituční šifru, která nahradí s B a naopak:
| Pár | Pravděpodobnost |
|---|---|
AA | 6,25% |
BB | 56,25% |
AB | 18,75% |
BA | 18,75% |
Celková pravděpodobnost náhoda v této situaci je 62,5% (6,25% pro AA + 56.25% na BB), přesně stejný jako u nezašifrované "holý" případ. Ve skutečnosti, nová abeceda produkovaný substituce je jen jednotná přejmenováním z původních znaků identit, které nemá vliv, zda se shodují.
Nyní předpokládejme, že pouze jedna zprávy (říci, druhé) jsou kódovány použitím stejného substituční kód (A, B) → (B, A). Následující dvojice může být nyní očekávat:
| Pár | Pravděpodobnost |
|---|---|
AA | 18,75% |
BB | 18,75% |
AB | 56,25% |
BA | 6,25% |
Nyní pravděpodobnost náhoda je pouze 37,5% (18,75% pro AA + 18.75% na BB). To je znatelně nižší než pravděpodobnost, kdy byly použity stejné-jazyk, stejný-abecedy texty. Je zřejmé, že náhody jsou pravděpodobnější, pokud nejčastější písmena v každém textu jsou stejné.
Stejná zásada platí pro skutečné jazyků jako je angličtina, protože některá písmena, jako E, se vyskytují mnohem častěji, než jiné dopisy-fakt, který se používá v frekvenční analýzu z substitučních šifer . Coincidences zahrnující písmeno E, například, jsou relativně pravděpodobné. Takže když se porovnávají všechny dva anglické texty, bude náhoda počet bude vyšší, než jsou-li použity anglické znění a cizího jazyka text.
To může být snadno představit, že tento účinek může být jemné. Například, podobné jazyky mají vyšší koincidenční počet než odlišných jazyků. Také, to není těžké vytvořit náhodný text s frekvenčním distribuce podobné skutečnému textu, uměle zvýšit koincidenční počet. Nicméně, tato technika může být efektivně využity k identifikaci, když se dva texty budou pravděpodobně obsahovat smysluplné informace ve stejném jazyce pomocí stejnou abecedu, objevovat období pro opakování kláves, a odhalit mnoho dalších druhů nenáhodné jevů v rámci nebo mezi ciphertexts.
Stejný nápad může být použita na jediném textu, kde vzorek je ve skutečnosti v porovnání s sobě . Matematicky můžeme spočítat index náhoda IC pro daný dopis-frekvenční distribuci jako

kde ![]() je délka textu a
je délka textu a ![]() prostřednictvím
prostřednictvím ![]() jsou frekvence (jako celá čísla) o
jsou frekvence (jako celá čísla) o ![]() písmena abecedy (
písmena abecedy ( ![]() pro monocase angličtině ). Součet
pro monocase angličtině ). Součet ![]() je nutně
je nutně ![]() .
.
Tyto výrobky ![]() počítat množství kombinací z
počítat množství kombinací z ![]() prvků o dva najednou.(Ve skutečnosti tento počítá každý pár dvakrát, že další faktory 2 se vyskytují v obou čitatele a vzorce, a tím se ruší.) Každý z
prvků o dva najednou.(Ve skutečnosti tento počítá každý pár dvakrát, že další faktory 2 se vyskytují v obou čitatele a vzorce, a tím se ruší.) Každý z ![]() výskytů
výskytů ![]() -tého písmene odpovídá každá ze zbývajících
-tého písmene odpovídá každá ze zbývajících ![]() výskytů stejným písmenem. Existuje celkem
výskytů stejným písmenem. Existuje celkem ![]() páry písmen v celém textu, a
páry písmen v celém textu, a ![]() je pravděpodobnost partner pro každou dvojici, za předpokladu, že jednotný náhodný rozdělení znaků ("null model", viz níže). Tak, tato rovnice udává poměr celkového počtu shodujících pozorovaných na celkovém počtu shodujících že by se očekávalo od nulové modelu. [ 2 ]
je pravděpodobnost partner pro každou dvojici, za předpokladu, že jednotný náhodný rozdělení znaků ("null model", viz níže). Tak, tato rovnice udává poměr celkového počtu shodujících pozorovaných na celkovém počtu shodujících že by se očekávalo od nulové modelu. [ 2 ]
Očekává průměrná hodnota pro IC mohou být počítány z relativních písmeny frekvencí ![]() na zdrojovém jazyce:
na zdrojovém jazyce:
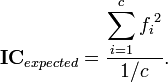
Pokud jsou všechny ![]() dopisy abecedy byly rovnoměrně rozděleny, by očekávaný index 1,0. Skutečný monografická IC pro telegrafické anglického textu je asi 1,73, což odráží nerovnosti přirozené jazykové dopisu distribucí.Očekávané hodnoty pro různé jazyky [ 3 ] jsou:
dopisy abecedy byly rovnoměrně rozděleny, by očekávaný index 1,0. Skutečný monografická IC pro telegrafické anglického textu je asi 1,73, což odráží nerovnosti přirozené jazykové dopisu distribucí.Očekávané hodnoty pro různé jazyky [ 3 ] jsou:
| Jazyk | Index shody okolností |
|---|---|
Angličtina | 1.73 |
Francouzština | 2.02 |
Němec | 2.05 |
Italština | 1.94 |
Portugalština | 1.94 |
Rus | 1.76 |
Španělština | 1.94 |
Někdy podobné hodnoty jsou uvedeny bez Normalizační jmenovateli, např. ![]() pro anglicky; tyto hodnoty mohou být navštíveny
pro anglicky; tyto hodnoty mohou být navštíveny ![]() ("kappa-plaintext"), spíše než "IC", s
("kappa-plaintext"), spíše než "IC", s ![]() ("kappa-random") používá k označení jmenovatele
("kappa-random") používá k označení jmenovatele ![]() (což je Očekává náhoda sazba pro rovnoměrné rozložení stejné abecedy,
(což je Očekává náhoda sazba pro rovnoměrné rozložení stejné abecedy, ![]() pro angličtinu).
pro angličtinu).
Výše uvedený popis je pouze úvodem do používání indexu koincidence, která se vztahuje k obecnému pojmu korelace . Různé formy indexu shody okolností byly vytvořeny, "delta" IC (podle vzorce výše) v podstatě měří autokorelačníjednoho distribuce, zatímco "kappa" IC se používá při spojení dvou textových řetězců. [ 4 ] Ačkoli v některých faktorech aplikace stálých jako ![]() a
a ![]() mohou být ignorovány, v obecnějším situacích existuje značná hodnota skutečněindexování každý IC proti hodnoty, která se očekává na nulové hypotézy(obvykle: žádná shoda a rovnoměrné náhodné symbol distribuce), tak, že v každé situaci očekávaná hodnota je 1,0 pro žádný korelace. Tak může být každý forma IC vyjádřit jako poměr počtu shodujících skutečně pozorovaných na počtu shodujících očekává (v závislosti na nulové modelu), za použití konkrétního nastavení testu.
mohou být ignorovány, v obecnějším situacích existuje značná hodnota skutečněindexování každý IC proti hodnoty, která se očekává na nulové hypotézy(obvykle: žádná shoda a rovnoměrné náhodné symbol distribuce), tak, že v každé situaci očekávaná hodnota je 1,0 pro žádný korelace. Tak může být každý forma IC vyjádřit jako poměr počtu shodujících skutečně pozorovaných na počtu shodujících očekává (v závislosti na nulové modelu), za použití konkrétního nastavení testu.
Z výše uvedeného, je snadné vidět, že vzorec pro kappa IC "je
![\ Mathbf {IC} = \ frac {\ displaystyle \ sum_ {j = 1} ^ {N} [a_j = b_j]} {N / c},](http://upload.wikimedia.org/math/f/7/c/f7ce27c5c7f47ae6507cda25c969a179.png)
kde ![]() je společný souladu délka obou textů a B , a bracketed termín je definován jako 1, pokud -th dopis textu odpovídá -tého dopis textu B , jinak 0.
je společný souladu délka obou textů a B , a bracketed termín je definován jako 1, pokud -th dopis textu odpovídá -tého dopis textu B , jinak 0.![]()
![]()
Příbuzné pojetí, "boule" z distribuce, měří rozdíl mezi pozorovanou IC a nulové hodnoty 1,0. Počet kódové abeced používaných v polyalphabetic kódu může být odhadnuta vydělením očekávaný výběžku delta IC pozorovanou vyboulení, i když v mnoha případech (například při opakování klíč byl použit) lepší techniky jsou k dispozici.
Jako praktickou ukázku používání IC, předpokládám, že jsme zachytili následující šifrový zpráva:
QPWKA LVRXC QZIKG RBPFA EOMFL JMSDZ VDHXC XJYEB IMTRQ WNMEA IZRVK CVKVL XNEIC FZPZC ZZHKM LVZVZ IZRRQ WDKEC Hosny XXLSP MYKVQ XJTDC IOMEE XDQVS RXLRL KZHOV
(Seskupení do pěti postav je jen telegrafické konvence a nemá nic společného se skutečnými slovo délky.) podezření, že se jedná o anglický plaintext šifrované pomocí Vigenère kód s běžnými A-Z komponentů a krátké opakující klíčovým slovům, můžeme zvážit ciphertext "naskládané" do nějakého počtu sloupců, například sedm:
QPWKALV RXCQZIK GRBPFAE OMFLJMS DZVDHXC XJYEBIM TRQWN ...
Pokud je klíč velikost se stane byly stejné jako předpokládaný počet sloupců, pak všechny dopisy v rámci jednoho sloupce bude muset být zašifrován používat stejný klíč dopis, ve skutečnosti jednoduché Caesarova šifra použije na náhodném výběru anglických znaků prostého textu . Odpovídající soubory písmen šifrového by měl mít drsnost rozdělení četností podobném tomu angličtiny, ačkoli písmeno totožnost byla deionizovaná (posunuty o konstantní výši odpovídající klíče písmeno). Proto, když počítáme celkovou delta IC pro všechny sloupce ("delta bar"), mělo by to být kolem 1,73. Na druhé straně, pokud se již nesprávně odhadl velikost klíče (počet sloupců), měl by být souhrnný delta IC být kolem 1,00. Takže počítáme delta IC pro převzatých klíčové velikosti jedna-deset:
| Velikost | Delta-bar IC |
|---|---|
1 | 1.12 |
2 | 1.19 |
3 | 1.05 |
4 | 1.17 |
5 | 1.82 |
6 | 0.99 |
7 | 1.00 |
8 | 1.05 |
9 | 1.16 |
10 | 2.07 |
Je vidět, že velikost klíče je pravděpodobně pět. Pokud skutečná velikost je pět, bychom očekávali, že šířku deseti také nahlásit vysoké IC, protože každý z jeho sloupců odpovídá i jednoduché zašifrování Caesar, a my to potvrzují.Takže bychom měli skládat ciphertext do pěti sloupců:
QPWKA LVRXC QZIKG RBPFA EOMFL JMSDZ VDH ...
Nyní můžeme pokusit určit nejpravděpodobnější klíč dopis pro každý sloupec posuzovaného zvlášť, provedením zkušební Caesar dešifrování celého sloupce pro každý z 26 možností-Z pro klíčové dopisu, a výběr klíčové dopis, který produkuje nejvyšší korelaci mezi dešifrovaných frekvencí sloupců písmen a relativní dopis frekvencí pro normální anglického textu. To korelace, které nemáme potřebu se starat o normalizaci, lze snadno vypočítat jako

kde ![]() jsou pozorované frekvence sloupců písmeno a
jsou pozorované frekvence sloupců písmeno a ![]() jsou relativní dopis kmitočty pro češtině. Když jsme zkusit, jsou ustavovací klíčové dopisy ohlásen být "
jsou relativní dopis kmitočty pro češtině. Když jsme zkusit, jsou ustavovací klíčové dopisy ohlásen být " KAŽDÝ , "které považujeme za skutečné slovo, a pomocí tohoto pro dešifrování Vigenère produkuje holý:
MUSTC HANGE MEETI NGLOC ACE FROMB RIDGE TOUND ERPAS SSINC EENEM YAGEN TSARE popírá VEDTO HAVEB EENAS Signe DTOWA TCHBR IDGES TOPME eting TIMEU NCHAN GEDXX
z nichž jeden získá:
Se musí změnit umístění setkání z mostu k podchodu OD nepřátelské agenty jsou považovány za byly přiřazeny DÁVAT BRIDGE STOP času schůzky beze změny XX
po divize slova byly obnoveny v zřejmých místech. " XX "jsou evidentně" null "znaky používané pro podložku z finálové skupině pro přenos.
Celý tento postup by mohl být snadno balí do automatizovaného algoritmu pro porušení těchto šifer. Vzhledem k běžné statistické fluktuace, bude takový algoritmus občas dělají špatná rozhodnutí, a to zejména při analýze krátké šifrový text zprávy.