Tabulka duha je precomputed tabulka pro couvání kryptografické hash funkce, obvykle pro krakování heslo hashe. Tabulky jsou obvykle používány při vymáhání holého textu hesla , až do určité délky se skládá z omezeného souboru znaků. Je to praktický příklad časoprostoru kompromis , používat méně zpracování v počítači času na úkor větší skladování ve srovnání k výpočtu hodnoty hash na každý pokus, nebo více času na zpracování a skladování méně ve srovnání s prostou vyhledávací tabulky s jedním vstupem na hash.Použití klíče derivačního funkce , které zaměstnávají sůl je tento útok nemožný.

Duha tabulky jsou zpřesnění dřívějšího, jednodušší algoritmus by Martin Hellman ^[ 1 ] .

[ editovat ]Pozadí

Každý počítač, který vyžaduje heslo ověření musí obsahovat databázi hesel, šifrované nebo prostý text . Zatímco různé metody heslo skladování existují, většina databází ukládat šifrovací hash z hesla uživatele v databázi. V takovém systému, není možné zjistit, jaké heslo uživatele je, prostě při pohledu na hodnotu uloženou v databázi. Místo toho, aby se zjištění, jaké heslo uživatele je, musí být nějaká způsobem, jak zabránit hash.

Duha tabulky jsou jedním z nástrojů, které lidé vyvinuli ve snaze přijít na to, co je heslo při pohledu pouze na hash hodnotu.

Duha tabulky nejsou vždy potřeba, protože je jednodušší metody hash reversal k dispozici. Brute-force attacks a slovníkové útoky jsou nejjednodušší metody k dispozici, ale ty nejsou vhodné pro systémy, které používají velké hesla, protože je obtížné i ukládání všech dostupné možnosti, a vyhledávání přes tak velké databáze provádět reverzní-lookup z hash.

Chcete-li tento problém vyřešit v rozsahu, Reverse Lookup tabulky byly generovány, že budou uloženy pouze menší výběr hash, že když obrátil by mohlo vytvořit dlouhé řetězce hesel. Přestože zpětného vyhledávání z hash v řetězech tabulce trvá déle výpočetní čas, může vyhledávací tabulky sám je mnohem menší, takže hashe delších hesel lze uložit. Duha tabulky jsou zdokonalení této techniky řetězení a poskytnout řešení problému s názvemřetězce kolizí .

[ upravit překlad ]Precomputed hash řetězce

Tato sekce není citovat žádnéodkazy nebo zdroje . (listopad 2010)

Poznámka: hash řetězce popsané v tomto článku jsou různé druhy řetězu, než které jsou popsány v hash řetězců článku.

Předpokládejme, že máme hesla hash funkce H a konečná množina hesel P. Cílem je precompute datová struktura, která vzhledem k tomu, libovolný výstuph na hašovací funkce, může buď najít element p v P takové, že H ( p ) = h , nebo určit, že není tam žádná taková p v P. Nejjednodušší způsob, jak to udělat, je výpočetně H ( p ) pro všechny p v P , ale pak ukládání tabulky vyžaduje Θ (| P | n ) bitů prostoru, kde n je velikost výstupu H, která je nepřístupná pro velké P.

Hash řetězy jsou techniky pro snížení tohoto potřebný prostor. Cílem je definovat funkce redukce R, která mapuje hodnoty hash zpět na hodnoty v P. střídáním hash funkce s funkcí redukce, řetězce jsou tvořeny střídavého hesla a hash hodnoty. Například, je-li P byl soubor malým abecední 6-znak hesla a hash hodnoty byly 32 bitů dlouhé, může řetěz vypadat takto:

Chcete-li generovat tabulku, zvolíme náhodnou sadu počátečních hesel z P, spočítat řetězy nějakého pevné délky k. Pro ​​každé z nich, a ukládat pouzeprvní a poslední heslo v každém řetězci. První heslo, se nazývá výchozí bod a poslední se nazývá koncový bod . V příkladu řetězce výše "aaaaaa" by být výchozím bodem a "kiebgt" by koncový bod, a žádný z ostatních hesel (nebo hodnoty hash) byly uloženy.

Nyní, vzhledem k tomu hash hodnota h , které chceme inverzi (najít odpovídající heslo pro), vypočítat řetěz začínající h za použití R, pak H, pak R, a tak dále.Pokud se v jakémkoliv okamžiku pozorovat hodnotu odpovídající jedné z koncových bodů v tabulce, dostaneme odpovídající výchozí bod a použít znovu řetězu. Je tu dobrá šance, že tento řetězec bude obsahovat hodnotu h , a pokud ano, bezprostředně předcházející hodnota v řetězci je heslo p , že se snažíme.

Například, pokud budeme stejně hash 920ECF10, bychom počítat jeho řetěz předtím použita R:

Vzhledem k tomu, "kiebgt" je jeden z koncových bodů v našem stolu, pak se odpovídající východisko heslo "aaaaaa" a postupujte podle jeho řetězce, dokud 920ECF10 je dosaženo:

Tak, heslo "sgfnyd".

Všimněte si však, že tento řetězec není vždy obsahovat hodnotu hash h , to může tak stát, že se řetěz začínající na h splývá s řetězci začíná na startu v určitém okamžiku po h . Například, můžeme být hodnoty hash FB107E70, a když jsme se pokračovat v jeho řetěz, dostaneme kiebgt:

Ale FB107E70 není v řetězci počínaje "aaaaaa". Toto se nazývá falešný poplach . V tomto případě, jsme ignorovat utkání a dále rozšířit řetězec h hledá jiném závodě. Pokud řetěz h dostane rozšířena na délku k. bez dobré zápasy, pak heslo byl nikdy produkován v některém z řetězců.

Obsah tabulky nezávisí na hash hodnotu, kterou chcete převrácený. Je vytvořen jednou a pak opakovaně použity pro nemodifikovaných vyhledávání. Zvýšení délku řetězce snižuje velikost tabulky. To také zvyšuje čas potřebný k provedení vyhledávání, a to je čas-paměť kompromis z tabulky duhového. V jednoduchém případě jedné položky řetězců, vyhledávání je velmi rychlý, ale tabulka je velmi velký. Jakmile řetězy se prodlužují, vyhledávání zpomaluje, ale velikost stolu jde dolů.

Jednoduché hash řetězce mají několik nedostatků. Většina závažné, pokud v každém bodě dva řetězy se srazí (produkují stejnou hodnotu), budou slučovat a následně tabulka nebude zahrnovat tolik hesel navzdory tomu, že zaplatil stejnou výpočetní náklady na generování. Vzhledem k tomu, předchozí řetězy nejsou uloženy v jejich plném rozsahu, to je nemožné detekovat efektivně.Například, v případě, že třetí hodnota v řetězci 3 odpovídá druhou hodnotu v řetězci 7, budou oba řetězce pokrývají téměř stejný sled hodnot, ale jejich konečné hodnoty nebude stejné. Hash funkce H Není pravděpodobné, že kolize, jak je obvykle považována za důležitou bezpečnostní funkci, která není k tomu, ale funkce redukce R, protože z jeho potřeby správně pokrytí pravděpodobné holé, nemůže být kolizi odolné.

Ostatní problémy vyplývají z významu výběru správného funkci R. Vysávání R být identita je jen o málo lepší než metodou hrubé síly. Pouze tehdy, když útočník má dobrou představu o tom, co se pravděpodobně holé budou si mohl vybrat funkci R, který zajistí, pouze čas a prostor jsou používány pro pravděpodobných holé není celý prostor možných hesel. Ve skutečnosti R pastýři výsledky předchozích výpočtů hash zpět k pravděpodobnému holé, ale tato výhoda je dodáván s nevýhodou, že R pravděpodobně nebude vyrábět všechny možné holý ve třídě útočník chce kontrolu popírající jistotu útočník, který bez hesel pochází z jeho vyvolené třída. Také to může být obtížné navrhnout funkční R tak, aby odpovídala očekávanému rozložení holé.

[ upravit překlad ]rainbow tables

Duha tabulky účinně řešit problém kolize s obyčejnými hash řetězců tím, že nahradí jednotné snížení funkce R se sekvencí souvisejících redukčních funkcí R ₁ až R _k. . Tímto způsobem, aby po dobu dvou řetězců se srazí a sloučit, musí zasáhnout stejnou hodnotu na stejném iteraci . V důsledku toho bude výsledné hodnoty v každém řetězci být totožné. V konečném znění postprocessing průchod může řadit řetězy v tabulce a odstranit veškeré "duplicitní" řetězy, které mají stejnou konečnou hodnotu jako ostatní řetězce.Nové řetězy jsou pak generovány vyplnit tabulku. Tyto řetězy nejsou bezkolizní(mohou částečně překrývat krátce), ale nebudou slučovat, výrazně snižuje celkový počet kolizí.

Pomocí sekvence změn redukčních funkcí, jak se provádí vyhledávání: protože hash hodnota podílu může být k dispozici na každém místě v řetězci, je nutné vytvořit k různým řetězců. První řetězec předpokládá, hash hodnota je v posledním hash pozici a jen platí R _k. , další řetězce předpokládá, hash hodnota je v druhý-k-poslední hash polohy a platí R _k. -1 , pak H, pak R _k. ; a tak dále, dokud poslední řetězec, který se použije všechny redukční funkce, střídající se s H. Tím se vytvoří nový způsob, jak produkovat falešný poplach: pokud se "hádat" pozice hash hodnoty nesprávné, můžeme zbytečně hodnotit řetězec.

Ačkoli duha tabulky mají následovat další řetězy, dělají se na to tím, že má méně tabulky: jednoduché mřížky řetězce tabulky nemůže růst nad určitou velikost, aniž by se rychle stává neefektivní kvůli spojujících řetězce, aby se s tím vypořádat, tvrdí více tabulek, a každý vyhledávání musí probírat každé tabulky. Duha stoly mohou dosáhnout podobný výkon s ​​tabulkami, které jsouk. krát větší, což jim umožní provést faktor kv vyhledáváními méně.

[ editovat ]Příklad

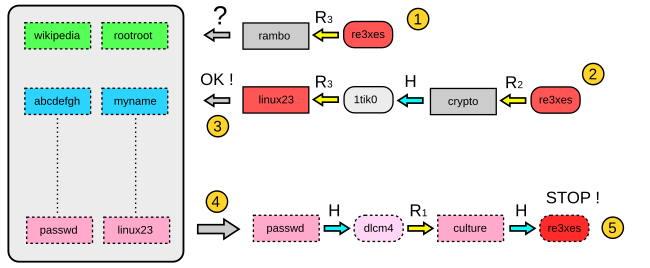
Máme hash ( re3xes ) a chceme najít jedno heslo, které produkuje tento hash.

1. Počínaje hash ("re3xes"), jeden počítá poslední snížení použitý v tabulce a kontroluje, zda je heslo se objevuje v posledním sloupci tabulky (krok 1).

2. Pokud se test nezdaří ( rambo nezobrazí v tabulce), jeden počítá řetězec s posledními dvěma snížení (tyto dvě slevy jsou zastoupeny v kroku 2)

   Poznámka: Pokud tento nový test znovu selže, jeden pokračuje s 3 snížení, 4 snižování, atd., dokud heslo nalezen. Není-li řetězec obsahuje heslo, pak útok selhal.

3. Pokud tento test pozitivní (krok 3, linux23 objeví na konci řetězce a v tabulce), je heslo získat na začátku řetězce, který vytváří linux23 . Zde se zde passwd na začátku příslušného řetězu uložené v tabulce.

4. V tomto bodě (krok 4), jeden generuje řetězec a porovnává na každé iteraci hash s cílovou hash. Test je platný, a najdeme hash re3xes v řetězci. Aktuální heslo ( kultura ), je ten, který vyrábí celý řetězec: útok je úspěšný.

Duha tabulky použít rafinovaný algoritmus s jiným snížení funkce pro každý "spojení" v řetězci, tak, že v případě, že je hash kolize ve dvou nebo více řetězců řetězy nebude sloučí tak dlouho, jak kolize nenastane současně pozice v každém řetězci. Stejně jako zvyšuje pravděpodobnost správného trhliny pro daný velikosti tabulky, toto použití více redukčních funkcí přibližně zdvojnásobuje rychlost vyhledávání. Podívejte se na papír uvedený níže.

Duha tabulky jsou specifické pro transformační funkci, které byly vytvořeny pro např., MD5 může prasknout tabulky pouze MD5 hashe. Teorie této techniky byl nejprve propagoval Philippe Oechslin ^[ 2 ] jako rychlý forma časově paměti kompromis , ^[ 3 ] , které se provádí v systému Windows cracker heslaOphcrack . Silnější RainbowCrack Program byl později vyvinut, které mohou vytvářet a používat rainbow tables pro různé znakové sady a algoritmy hash, včetně hash systému LM , MD5 , SHA1 , atd..

[ editovat ]Obrana proti tabulek duhových

Tabulka duha je neúčinný proti jednosměrné hash, které zahrnují soli .Například, zvažovat hash hesla, který je generován pomocí následující funkce (kde " + "je zřetězení operátor):

saltedhash (heslo) = hash (heslo + sůl)

Nebo

saltedhash (heslo) = hash (hash (heslo) + salt)

Sůl hodnota není tajné a mohou být generovány náhodně a uloženy s heslem hash. Velké slané hodnota zabraňuje předpočítání útoky, včetně duhových tabulek, tím, že každý uživatel heslo je zatříděna jednoznačně. To znamená, že dva uživatelé se stejným heslem bude mít jiné heslo hashe (za předpokladu, že různé soli se používají). Ve snaze uspět, útočník potřebuje precompute tabulek pro každou možnou hodnotu soli. Sůl musí být dostatečně velký, jinak útočník může vytvořit tabulku pro každou sůl hodnotu. Pro starší Unix hesel , které používaly 12-bit sůl To by vyžadovalo 4096 tabulky, významné zvýšení nákladů pro útočníka, ale není nepraktické s terabajt pevných disků. V md5-crypt a bcrypt metody použity v Linuxu , BSD Unix, a Solaris -mají soli 48 a 128 bitů, resp. ^[ 4 ] Tyto větší sůl hodnoty, aby předpočítání útoky pro téměř všechny délky hesla neproveditelné proti těchto systémů pro v dohledné budoucnosti.

Další technika, která pomáhá předcházet předpočítání útoků je klíčem strečink. Je-li použito strečink, jsou sůl, heslo, a počet přechodných hash hodnot projít podkladových hash časů funkce více pro zvýšení výpočetní čas potřebný k hash každého hesla. ^[ 5 ] Například, md5-crypt používá 1000 iteraci smyčky, které opakovaně krmí sůl, heslo a aktuální zprostředkující hodnotu hash zpět do základní MD5 hash funkce. ^[ 4 ] Heslo uživatele hash je zřetězení soli hodnoty (což není tajné) a konečné hash. Čas navíc není patrný na uživatele, protože uživatel musí pouze čekat zlomek druhého pokaždé, když uživatel přihlásí Na druhou stranu, natahovat výrazně snižuje účinnost několika brute-force nebo předpočítání útoky, protože snižuje Řada výpočtů útočník může provést v daném časovém rámci. Tato zásada se uplatňuje v md5-crypt a bcrypt. ^[ 6 ]

Alternativní přístup, tzv. klíčové posilování , rozšiřuje klíč s náhodným solí, ale pak (na rozdíl od klíči strečink) bezpečně odstraní soli. Tato síly jak útočník a oprávněným uživatelům provádět brute-force hledání soli hodnoty. ^[ 7 ] Ačkoli papír, který zavedl šipky strečink ^[ 8 ] podle této dřívější techniky a záměrně si vybral jiný název, termín "klíčové posilování "je nyní často (pravděpodobně nesprávně) používán odkazovat se na zadávat strečink.

Duha stoly a jiné předpočítání útoky nefungují proti hesel, které obsahují symboly mimo předpokládaného rozsahu, nebo které jsou delší než ty, které Precomputed útočníkem. Nicméně tabulky mohou být generovány, které berou v úvahu způsoby společných, ve kterých se uživatelé pokusí vybrat více bezpečná hesla, například přidáním čísla nebo speciálního znaku. Vzhledem k značnému investice do zpracování výpočetní, duhové tabulky mimo čtrnáct míst v délce ještě nejsou běžné. Takže, může vybrat heslo, které je delší než čtrnáct znaků nutí útočníkovi uchýlit k brute-force metod.^{[ pochvalná zmínka potřebovaný ]}

Některé intenzivní úsilí zaměřené na LM hash , starší hashovací algoritmus používá společnost Microsoft, jsou veřejně dostupné. LM hash je obzvláště zranitelní, protože hesla delší než 7 znaků jsou rozděleny do dvou částí, z nichž každá je zatříděna odděleně. Výběr hesla, které je patnáct znaků nebo delší záruky, že LM hash nebude generovány. ^[ 9 ]

[ editovat ]Společné použití

Téměř všechny distribuce a variace Unix , Linux , a BSD použití hash systému s solí, ačkoli mnoho aplikací používá jen hash (typicky MD5 ) bez soli.Microsoft Windows NT/2000 rodina používá správce LAN a NT LAN Managerhash metody a je také nesolené, které z něj činí jeden z více populárně vytvořených tabulek.