Signál

Tento článek pojednává o obecné fyzikální veličině závislé na čase. Další významy jsou uvedeny v článku Signál (rozcestník).

Signál (z lat. signum, znamení a signalis - užitý jako znamení) je fyzikální veličina závislá na čase. Díky signálům lze přenášet zprávy – data. Může se tak jednat například o signály optické, elektrické, elektromagnetické, akustické,mechanické, pneumatické, nebo hydraulické.

Rozdělení signálů

Z hlediska trvání signálu

Kauzální signál - Takový signál, který do svého počátku v časovém okamžiku měl nulovou hodnotu, je signál kauzální.
.

· finitní - Signál je definovaný na časovém intervalu $t\in<t_0;t_1>$ a vně tohoto intervalu je nulový. $s(t)=0, pro: t\in<t_0;t_1>$ .

· infinitní - Signál je definovaný na časovém intervalu $t\in<t_0;\infty)$ .

Nekauzální signál je takový signál, který nesplňuje podmínku kauzality. Například jde o periodické funkce sinus, kosinus.

Z hlediska definičního oboru

Signál ve spojitém čase je definovaný pro všechny okamžiky na intervalu: $t\in(-\infty;\infty)$ . Jde tedy o nespočetnou množinu časových okamžiků.

Signál v diskrétním čase, je definován jen pro určité časové okamžiky z čehož plyne, že se jedná o spočetnou množinu. Pro čas platí: $t\in\{t_k\}_{k\in(-\infty;\infty),k\in\mathbb{N}}$ . Takový signál je označovaný jako , , případně jako posloupnost $\{s_k\}$ . Index k pak určuje pořadí vzorku signálu. Často je použit ekvidistantní krok vzorkování.

Z hlediska determinovanosti signálu

Determinovaný signál - je takový signál u nějž lze určit hodnotu v jakýkoliv okamžik s absolutní jistotou.

· periodické - signál je definovaný pro $t\in(-\infty;\infty)$

· harmonické

· neharmonické

· neperiodické

Stochastický signál - velikost signálu v libovolném okamžiku, dovedeme určit pouze s nějakou pravděpodobností.

· stacionární - nejsou závislé na poloze počátku časové osy.

· ergodické

· neergodické

· nestacionární - jsou závislé na poloze počátku časové osy.

Existují signály, které nejsou deterministické ani stochastické.

Přiřazení do určité kategorie není absolutní. Pro jednu stranu, která signál vysílá může být signál deterministický, ale pro stranu, která signál přijímá už deterministický být nemusí. Pokud by byl pro přijímací stranu deterministický, tak by si ho mohla sama generovat a nemusela ho přijímat.

V případech, kdy je deterministický popis signálu příliš složitý se může vyplatit zpracovávat jej jako stochastický signál.

Z hlediska spojitosti amplitudy signálu

· Signál se spojitou amplitudou

· Signál s nespojitou(diskrétní) amplitudou

Z hlediska integrability

Výkonové signály - Jsou takové pro něž existuje konečná a nenulová limita:
$\lim_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} |s(t)|^2\mathrm{d}t$

Energetické signály - Jsou takové pro něž existuje konečná a nenulová limita:
$\lim_{T \to \infty}\int_{-T}^{T} |s(t)|^2\mathrm{d}t$ Za povšimnutí stojí použití absolutní hodnoty, protože signál může být z oboru komplexních čísel.

Charakteristiky determinovaných signálů

Střední hodnota

Střední hodnota spojitého signálu na konečném časovém intervalu $t\in <t_a;t_b>$ :
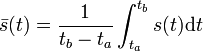
$\bar{s}(t)= \frac{1}{t_b-t_a}\int_{t_a}^{t_b}s(t)\mathrm{d}t$
Vyjadřuje průměrnou hodnotu signálu po dobu trvání intervalu. V souvislosti se signálem a jeho střední hodnotou by nás mohla zajímat fluktuace signálu: $\Delta s(t)=s(t)-\bar{s}(t)$ .

Střední hodnota posloupnosti signálu $\{s_k\}$ na konečném časovém intervalu $t\in <t_a;t_b>$ :
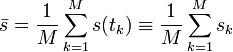$\bar{s}=\frac{1}{M}\sum_{k=1}^M s(t_k)\equiv\frac{1}{M}\sum_{k=1}^M s_k$ , kde $t_k\in<t_a;t_b>$
, kde k je pořadí vzorku a M je počet vzorků.

Energie signálu

Jednotkou energie signálu ve spojitém čase je $[\mbox{jednotka signalu}]^2 \cdot s$ a v diskrétním čase $[\mbox{jednotka signalu}]^2$ . Protože nejde o energii ve fyzikálním slova smyslu, není jednotkou energie signálu Joule.. Pokud je signálem například napětí je jednotkou energie signálu v diskrétním čase , pokud by byl použitý proud pak by jednotkou energie signálu ve spojitém čase byl $A^2\cdot s$ .
Energie signálu ve spojitém čase na konečném intervalu $t\in <t_a;t_b>$ :
$e[s(t)]= \int_{t_a}^{t_b}|s(t)|^2\mathrm{d}t$
Energie signálu $\{s_k\}$ v diskrétním čase na konečném intervalu $t\in <t_a;t_b>$ :
$e[\{s_k\}]= \sum_{k=1}^M |s_k|^2$

Vzájemná energie signálů

Vzájemná energie signálů ve spojitém čase na konečném intervalu $t\in <t_a;t_b>$ :
$e[u(t),v(t)]= \int_{t_a}^{t_b}|u(t)\cdot v^*(t)|\mathrm{d}t$

Výkon signálu

Podobně jako u energie signálu nebyl jednotkou Joule, není jednotkou výkonu signálu Watt, ale kvadrát fyzikálního rozměru signálu.
Výkon signálu ve spojitém čase na konečném intervalu $t\in <t_a;t_b>$ : $p[s(t)]= \frac{1}{t_b-t_a}\int_{t_a}^{t_b}|s(t)|^2\mathrm{d}t$

Vzájemný výkon signálů

Vzájemný výkon signálů ve spojitém čase na konečném intervalu $t\in <t_a;t_b>$ :
$p[u(t),v(t)]= \frac{1}{t_b-t_a}\int_{t_a}^{t_b}|u(t)\cdot v^*(t)|\mathrm{d}t$

Výkon střední hodnoty a fluktuace signálu

$p[\bar{s}(t)+\Delta s(t)]= \frac{1}{t_b-t_a}\int_{t_a}^{t_b}|\bar{s}(t)+\Delta s(t)|^2\mathrm{d}t=|\bar{s}(t)|^2+\frac{1}{t_b-t_a}\int_{t_a}^{t_b}|\Delta s(t)|^2\mathrm{d}t+\frac{2 \cdot \bar{s}(t)}{t_b-t_a}\int_{t_a}^{t_b}|\Delta s(t)|\mathrm{d}t=p[\bar{s}(t)]+p[\Delta s(t)]$
Zde je vidět, že výkon signálu je součtem výkonu jeho střední hodnoty a výkonu jeho fluktuace. Přenáší-li zprávu pouze fluktuace signálu je výhodné vysílat signál s nulovou střední hodnotou.

Periodicita

Pro periodický signál ve spojitém čase , existuje takový časový interval, že platí:
$s(t)=s(t+mT_0); t\in(-\infty;\infty), \forall m\in\mathbb{Z}$
Ze zápisu je patrné, že periodický signál je periodický i pro intervaly a další. Má tedy nekonečně mnoho period. Nejmenší z těchto period nazývámezákladní periodou.^[2] Pro operace sčítání, odečítání, násobení a dělení dvou signálů se stejnou periodou platí, že výsledkem je periodický signál se shodnou periodou.

Pro posloupnost periodického signálu v diskrétním čase $\{s_k\}$ platí, že existuje takové číslo u nějž platí:
$\{s_k\}=\{s_k+mN_0\}; N_0 \in \mathbb{Z},\forall m\in\mathbb{Z}$
Posloupnost je periodická i pro a další. Číslo je základní perioda.

Harmonický signál

Harmonický signál je takový signál, který lze vyjádřit funkcí $f(t) = A\sin(\omega t + \varphi_0)$ .

Charakteristika rozdělení přenosu signálu

podle charakteristiky signálu

· Přenos signálu lze rozdělit podle jeho charakteristiky na dva druhy:

· analogové informace analogovým signálem (například rozhlas, televize, telefon, hlas)

· digitální informace pomoci analogového signálu

Nevýhoda prvního druhu přenosu je menší odolnost vůči šumu, zkreslení apod. Pro druhý druh přenosu je třeba převést digitální signál na analogový při vysílání a zpět při přijímání.

podle množství informace

· Přenos signálu pak také lze dělit podle toho, zdali je v jeden okamžik vysílána:

· pouze jedna hodnota - sériový přenos

· nebo více hodnot - paralelní přenos

Paralelní přenos je oproti sériovému přenosu sice rychlejší, nicméně je nákladnější.

podle způsobu komunikace

· Přenos signálu můžeme rozdělit ještě

· synchronní

· asynchronní

Při synchronním přenosu je vysílač s přijímačem synchronizován tak, aby bylo zcela jasné, kdy se budou přenášet jednotlivé části příslušné informace. Při asynchronním vysílání vysílač vysílá bez ohledu na stav přijímače.

Zvláštní významy

V různých oborech se mohou signály používat k různým účelům.

Doprava

V dopravě se používají různé signály, které předávají účastníkům provozu informace o dopravě a řídí jejich chování

· semafory, signály pro tramvaje, železniční návěsti

· výstražné znamení (kupř. poplachová siréna, lodní píšťala, varovný výstřel z lodního děla, vyzvánění zvonů či zvonků, elektrická lokomotivní houkačka, elektrický zvonek u tramvají, barevné světlice, klakson motorového vozidla)

· právo přednosti v jízdě, pracovní vozidla (modrý majáček, červený majáček, oranžový majáček)

· signalizace používaná v lodním provozu (kupř.vlajková abeceda, signalizace z majáků atd.)

· velmi významná je také signalizace používaná v letecké dopravě (kupř. při provozu na letištích)

· u motorových vozidel kupř. blikače, znamení změny směru jízdy, brzdová světla varují o zpomalení vozidla

Informatika, elektronika, počítače

V informatice je pojem signál zobecněn a již není potřeba definovat fyzikální prostředí pro přenos informace.

Vojenství

V armádě se signály používají pro účely velení, komunikace a informovánívojenských jednotek. Významný je u všech typů vojsk, speciální systém signalizace je užíván kupř. ve válečném námořnictvu či ve vojenském letectví.

Politika

Pokleslý a zjevně zdegenerovaný význam slova, zjevná politická floskule. Je používán ve smyslu vzájemného předávání (povětšinou neoficielních) informací a pokoutních „zpráv“ (často šířených velmi nejasnou cestou) např. mezi politiky, státními úředníky, žurnalisty a novináři apod.