Strojové učení:
Základní přehled a terminologie

O čem je tedy strojové učení?

• Nejtypičtější úlohy jsou z oblasti učení s učitelem (supervised learning).

• Jsou dány: – vstupní veličiny (příznaky) X – výstupní veličina y (nebo g). Cílem je vytvořit model M, který co nejlépe postihne závislost výstupní veličiny y (g) na vstupech (příznacích) X, tedy 𝒚 =M(X)

• 𝒚 (𝒈 ) značí výstup modelu

• Snahou je model M nastavit tak, aby pro nová data ideálně 𝒚 =y (𝒈 =g)

Takže cílem SU je vytvořit model?

Velmi často. Celé je to poněkud složitější, ale u většiny úloh s učitelem je výsledkem model a odhad jeho přesnosti.

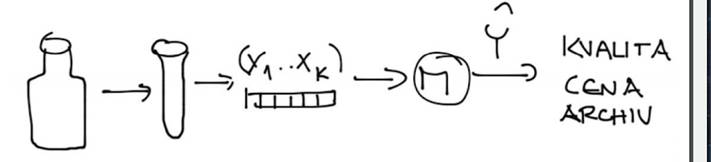
A na co je to dobré u vína? Pokud model máte, můžete odhadnout, jak je vaše víno kvalitní, nasadit tu „správnou“ cenu na trhu, zamyslet se nad úpravou procesu výroby nebo zcela v rozporu se zákonem nad úpravou vína již hotového… A to vše lze automatizovat (nakonec jsme ústav automatizace…).

Definice (strojového) učení

• učení je schopnost zlepšování výkonnosti (=přesnost modelu) tím, jak vzrůstá znalost (=nastavení parametrů modelu) na základě zkušenosti (=data)

• strojové učení je nauka o nástrojích (algoritmech, programech), které umožňují učení umělých objektů (artefaktů)

• program se učí pomocí zkušenosti E vzhledem k nějaké třídě úloh T a míře výkonnosti P, pokud se jeho výkonnost pro dané úlohy v T měřená pomocí P zlepšuje použitím E

• memorování není učení – nezahrnuje proces indukce.

Dva základní typy problémů

• učení s učitelem
– je známa výstupní veličina y (g)
– predikce (regrese, klasifikace)

• učení bez učitele

– není známa výstupní veličina, pouze vstupní X
– hledání shluků (hypotetických tříd) či souvislostí v datech

Rozdíl mezi umělou inteligencí a strojovým učením

Strojové učení nabízí matematický aparát a algoritmy, které jsou používané na řešení v úloh umělé inteligence.

Strojové učení vs. Umělá inteligence

Dolování dat a dobývání znalostí z databází

• Strojové učení je jako matematika – nabízí efektivní aparát na řešení různých problémů, žádným konkrétním se však nezabývá.

• KDD (dobývání znalostí z databází) i DM (dolování dat) jsou procesy, jejichž cílem je získání nové znalosti či informace z rozsáhlé databáze (v literatuře uváděné definice jsou takřka identické, více v samostatné přednášce věnované této problematice).

• KDD provozuje ten, kdo vlastní data a problém a bude profitovat z řešení, tedy z nalezené znalosti (v obchodu, provozu, …).

• DM provozuje ten, kdo má know-how ve strojovém učení; dostane vybraná historická data a úloha pro něj končí předáním nové znalosti.

• Někdy KDD a DM dělá ta samá osoba/tým/pracoviště, potom rozdíly mezi oběma termíny mohou splývat v jedno a to samé.

Proces modelování s učitelem

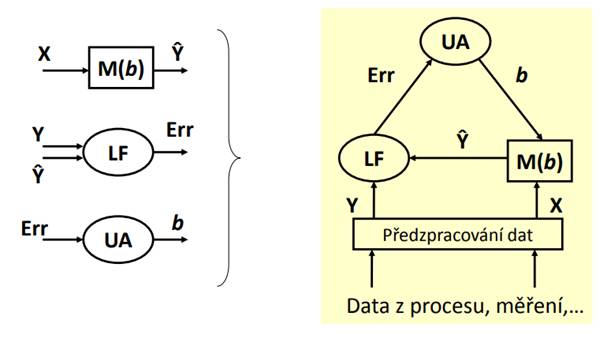
Komponenty procesu „modelování“

1) data X,Y,Ŷ (kvantitativní, kvalitativní)

2) předzpracování (ouliers, chybějící data, relevantní atributy, rozšíření příznakového prostoru)

3) model M (NS, rozhod. stromy, regresní modely) mající parametry b

4) chybové funkce LF (MNČ, ML, entropie) vracející chybu predikce Err

5) učicí algoritmy UA (optimalizační algoritmy; (ne)lineární prog., kvadratické, parametrické,..)

6) testy (cross-validation, bootstrap)

7) meta algoritmy (boosting, bagging, stacking)

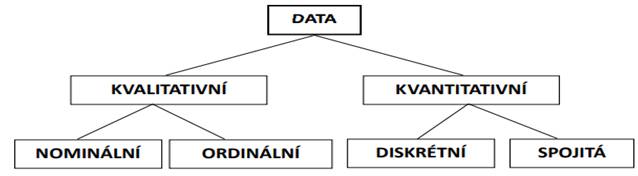
DATA – základní dělení, značení

• kvantitativní
– spojitá
– diskrétní

• kvalitativní
– nominální
– ordinální

• X – vstupní proměnná, nezávislá veličina, prediktor, vysvětlující proměnná

• y – kvantitativní výstupní veličina, závislá veličina, cílový atribut, vysvětlovaná proměnná
• G – kvalitativní výstupní veličina
• Ŷ – predikovaná kvantitativní veličina
• Ĝ – predikovaná kvalitativní veličina

DATA – další dělení

• specifické typy
– text, datum, dichotomická/binární, …

• data: čistá / zašuměná

• data: konzistentní / nekonzistentní

• doména (atributy): otevřená / uzavřená

• vzory: pozitivní / pozitivní i negativní

Data, Informace, Znalost, Moudrost…

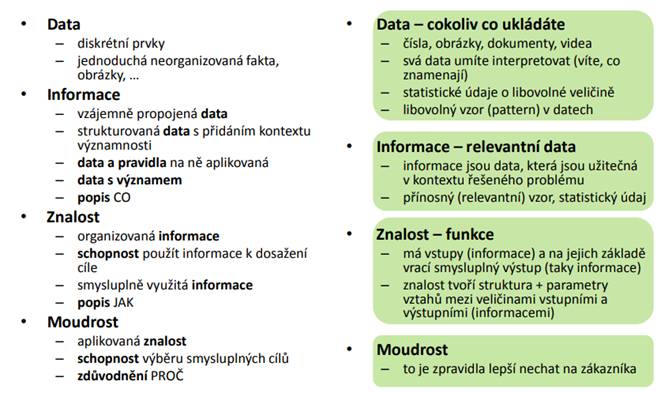
DATA v SU – od dat k metaznalosti

MODEL

• model (též znalost, funkce, hypotéza) je z pohledu SU matematicko-logická reprezentace zařízení nebo procesů, do jejíž struktury a parametrů jsou uloženy znalosti získané z analyzovaných dat

• regresní modely (výstup – kvantitativní data)

• klasifikátory (výstup – kvalitativní data)

• regresní klasifikátory

CHYBOVÁ FUNKCE

• smyslem chybové funkce je kvantifikovat míru odchylky výstupu modelu (Ŷ nebo Ĝ) oproti požadované hodnotě (Y nebo G)

• metoda nejmenších čtverců (MNČ)

• maximální věrohodnost (ML)

• nákladová matice (cost matrix)

• regularizace – penalizace za složitost modelu, zabraňuje přeučení

UČICÍ (OPTIMALIZAČNÍ) ALGORITMY

• smyslem učicích algoritmů je měnit parametry modelu tak, aby minimalizovaly hodnotu chybové funkce

• prakticky se jedná o prohledávání prostoru možných řešení

• některé metody:
– analytická/heuristická řešení
– gradientní metody
– simplexová metoda
– genetické algoritmy
– mravenčí kolonie, žíhání, …

Přesnost modelu

• přesnost modelu lze pouze odhadnout

• rozdělení dat
– trénovací
– (verifikační)
– testovací

• metody odhadu chyby
– cross
–validation
– bootstrap

Meta–algoritmy

• též meta-learning nebo ensemble methods

• meta-learning tvoří algoritmy, které umožňují predikovat na základě rozhodnutí více modelů

• vstupem do meta-modelu je 𝒀 , nikoliv X

• metody
– bagging
– boosting
– stacking

Teorémy SU

• occamovo ostří: nejjednodušší z více stejně přesných řešení je správné. Analýza oprávněnosti generalizace přesahující naměřená data.

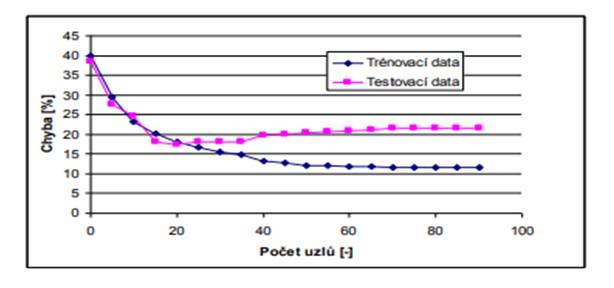
• přeučení modelu: přesné naučení modelu na trénovací data vedoucí k naučení šumu nebo neexistujících souvislostí; projeví se velkou chybou na testovacích datech

• kapacita funkce: (Vapnik-Chervonenkis)

Některé další pojmy

• indukce – přechod od konkrétního k obecnému (od dat ke znalostem); algoritmy SU jsou induktivního charakteru, platné vždy jen s určitou pravděpodobností; (důsledek – důvod)

• dedukce – přechod od obecného ke konkrétnímu (od znalostí k datům, novým řešením), platné s jistotou (pokud jsou předpoklady pravdivé); (důvod - důsledek)

Nákladní ideu učení s učitelem lze nalézt např. v tomto úryvku (Sir Arthur Conan Doyle: Poslední poklona Sherlocka Holmese, povídka Vila Vistárie): "Domníváte se, milý Watsone, že lidský důmysl dokáže najít VYSVĚTLENÍ, které by zahrnovalo OBĚ tyto SKUTEČNOSTI? Jestliže by pak takové vysvětlení nevylučovalo ani onen TAJUPLNÝ LÍSTEK, tak prazvláštně stylizovaný, stálo by za to, přijmout jej jako DOČASNOU HYPOTÉZU. Kdyby se VŠECHNY NOVÉ SKUTEČNOSTI, jež se dozvíme, HODILY DO JEJÍHO SCHÉMATU, možná že by se postupně ta hypotéza změnila v ODHALENOU PRAVDU."

• heuristika – iterační stochastický postup, nová iterace ovlivněna zkušeností z předešlých iterací.

Bias a Variance

• bias(předpojatost)
– odchylka konceptu modelu od skutečných vazeb (závislostí) v datech
– systematická chyba
– jak přesně odpovídá model skutečnosti
– existuje i při nekonečném množství dat

• variance
– chyba naučení dílčího modelu z konečné množiny dat
– odchylka od bias způsobená nedostatkem dat, nebo nevhodným výběrem z dat (není „ideální“)

• chyba modelu = bias+variance (rozbor označován ang. termínem bias-variance decompostition)

Generalizace

• jedním ze základních požadavků na model je jeho generalizace = zobecnění, obecně platný popis vazeb mezi vstupy a výstupy získaný z dat

• rozlišujeme tři typy generalizace hypotéz (modelů)
– jiná sudá čísla než 2 nejsou prvočísla správná generalizace
– přirozená čísla končící na 1 jsou prvočísla neoprávněná generalizace
– žádné prvočíslo není větší než 100 podceněná generalizace

Metoda prostoru hypotéz (verzí)

• metoda pracuje průběžně se dvěma hypotézami (modely) pomocí specializace a generalizace

• oba modely popisují všechny pozitivní prvky a vylučují všechny negativní prvky

• první model
– co nejspecifičtější
– s přibývajícími pozitivními prvky dochází k jeho generalizaci

• druhý model
– co nejobecnější
– s přibývajícími negativními dochází k jeho specializaci

Metoda prostoru verzí – tvorba hypotézy

• na počátku 2 modely, zcela speciální a obecný • každý nový model je specializací (generalizací) modelu obecného (speciálního)

• úprava vždy minimální možnou změnou

• žádný nový speciální (obecný) model není generalizací (specializací) jiného specifického (obecného) modelu

• záporný příklad – úprava specializací (obecného)

• kladný příklad – generalizace (speciálního)

• vyškrtni nevyhovující specifické modely

Příklad 1 – princip induktivního učení

• pozitivní případ – minimálně generalizuj

• negativní případ – minimálně specializuj

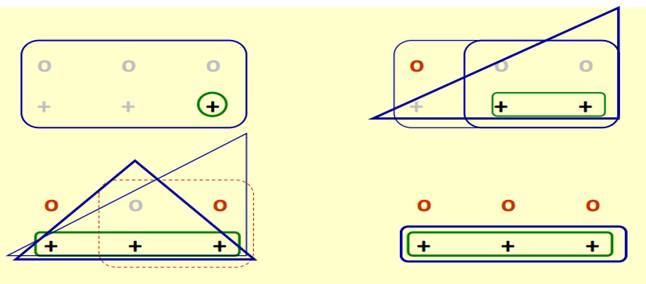
Příklad 2 – induktivní učení

Lékař léčí pacienta, který občas trpí diarrheou. Intuitivně předpokládá, že tyto souvisejí s místem stravování pacienta. Následující tabulka zahrnuje informace, které byly získány od pacienta.

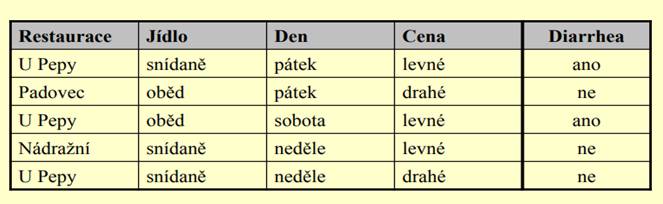
Příklad 2 – význam předpojatosti

• označme X množinu všech úplných instancí (hodnoty všech atributů jsou definovány). Pak mohutnost X = |X|= 3×2×3×2 = 36

• konceptem je v binární klasifikaci rozuměna hypotéza (soubor hypotéz) určující prvky jedné třídy (všechna xÎX jedné třídy)

• počet všech možných konceptů = počet podmnožin X = mohutnost potenční množiny P(X)= 2|X| =236 » 1010

• při použití uvedené metody lze zapsat jen 4×3×4×3=144 konceptů; metoda je předpojatá, má schopnost generalizace

• u metody umožňující popis každého konceptu hrozí riziko přeučení (tzv. unbiased learner, např. rozhodovací strom bez prořezávání)

• bez předpojatosti by nedošlo k žádné generalizaci, byla by uložena pouze trénovací data